The Mosaic function in Geographic Imager merges multiple georeferenced images together to create a single composite georeferenced image. Though the goal of the mosaic is to create a single and seamless composite image, combining images with the Mosaic tool will often result in a slight shift of the imagery due to differences in the original pixel registration grid. This means that even when images are in the same coordinate system with the same spatial resolution, error can still be introduced because of a difference in the pixel alignment. Due to this, mosaicking processes in general tend to produce results that may be very close, but not exact. With this in mind, the results of your mosaic may be improved by resampling your images beforehand to the smallest unit of the resolution.
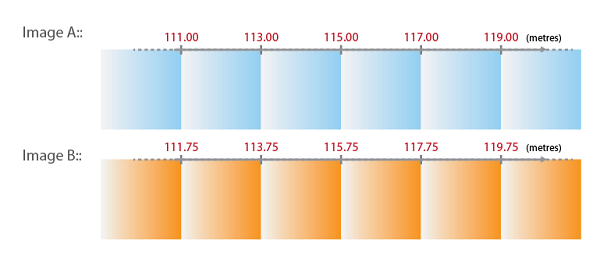
As an example, let’s say we have an image where the pixel size is 2.00 metres. When plotting the X coordinates of every pixel in this image (using the top left corner of the pixel), the X coordinate value will be incremented by the number/distance of the pixel size. For example, if the X coordinate values were to start at 111.00, then the next pixel would be 113.00, 115.00, 117.00, and so on. It’s important to note that these coordinate values are discrete, which means that the values could not be 113.22 or 115.77 because the origin of the coordinate in this case starts at 111.00 metres.

Now, we have another image that we want to mosaic with the first image. In this instance, the first image will be “Image A” and the second image will be “Image B”. Image B has the same coordinate system as well as the same pixel size as Image A.
Take a look at the X coordinates in Image A and Image B below:

We can see that the X coordinate in the top-left corner is different between these two images, and as previously mentioned, we know that the X coordinate values are discrete. When mosaicking Image B to Image A, the X coordinate cannot be 111.75 or 113.75. The coordinates must be 111.00, 113.00, 115.00, and so on, following the pattern of the pixel grid values in Image A.
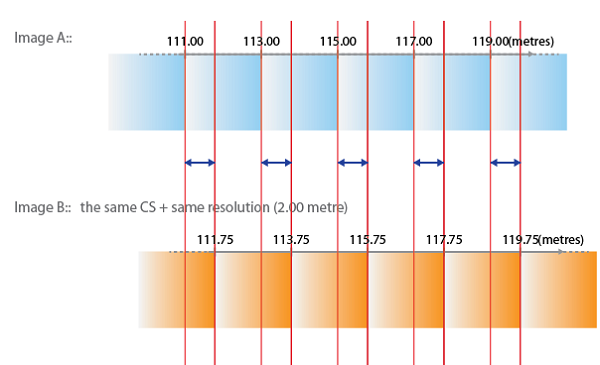
This means that Image B will need to be “shifted” or “snapped” to the closest coordinates when the mosaic is performed, see below:

As a result, the X coordinate of Image B will be shifted by 0.75 metres (less than half a pixel). The pixel with X coordinate 111.75 is now placed at 111.00 and the next pixel with X coordinate of 113.75 will now be placed at 113.00, and so on.
With this in mind, the results of your mosaic may be improved by resampling your images to the “smallest unit of the resolution”. The smallest unit of the resolution can be determined from the difference in the coordinates (spatial alignment difference) between the two images.
Looking back at our example, we can see that the smallest unit of the resolution (represented by the blue arrow) in this case is 0.75 metres – this is the value we will use to resample our images.
Once the images have been resampled to 0.75 metres, we may go ahead with our mosaic.
The above example demonstrates the possibility of a pixel shift after a mosaic for two images with a different pixel alignment. It should be noted that this example explains the problem in one-dimension (looking at only the X coordinate) when the image in reality is in two-dimension (looking at both X and Y coordinates). The basic principal of the pixel shift in 2D is the same, but it would include the direction of the shift when mosaicking images. In addition, it’s important to keep in mind that although resampling your images to the smallest unit of the resolution will improve the final mosaic, this is not always an efficient process when mosaicking with more than two images. Another thing to remember is that resampling your images will make your file size much larger. However, in cases where high precision is desired, resampling the images beforehand is a process that should be considered.